Разделы сайта

• Главная
• Исследования и анализ современных технологий
• IP-телефония
• Антенно-фидерные устройства
• Виртуальное построение рабочей локальной сети
• Влияние электромагнитного поля на подземную проволочную антенну
• Микрополосковая антенная решетка
• Система экологического мониторинга вредных газовых выбросов
• Организация процесса производства цифрового телевиденья

Анализ устойчивости системы

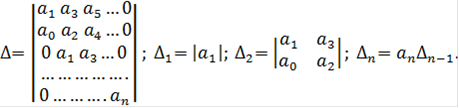
Критерий Гурвица формулируется следующим образом: для того чтобы замкнутая система была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого характеристического уравнения замкнутой системы . Мерседес сервис спб крук сервис диагностика мерседес в спб.

Применим алгебраический критерий Гурвица для замкнутой нескорректированной системы. Для этого в пакете MatLab найдем ее детерминант (функция det). Затем, последовательно уменьшая размер матрицы, найдем значения всех диагональных детерминантов.

Посчитаем передаточную функция разомкнутой системы

Расчёт в пакете MatLab:

>> wrazsis=wup*we*wm*wredfunction:

0.1673

-----------------------------------------

.003763 s^4 + 0.09328 s^3 + 0.658 s^2 + s

Передаточная функция замкнутой системы

Построение характеристического полинома замкнутой системы и нахождение определителей:

>> A=[0.09328 1 0 0; 0.003763 0.658 0.1673 0; 0 0.09328 1 0; 0 0.003763 0.658 0.1673]=

0.0933 1.0000 0 0

0.0038 0.6580 0.1673 0

0 0.0933 1.0000 0

0 0.0038 0.6580 0.1673

>> det(A)=

0.0094

>> A1=A(1:2,1:2)=

0.0933 1.0000

0.0038 0.6580

>> det(A1)=

0.0576

>> A2=A(1:3,1:3)=

0.0933 1.0000 0

0.0038 0.6580 0.1673

0 0.0933 1.0000

>> det(A2)=

0.0562

Как видно, все определители >0. Замкнутая нескорректированная система устойчива.

Анализ устойчивости с использованием частотного критерия Найквиста

Критерий устойчивости Найквиста позволяет судить об устойчивости замкнутой системы по поведению АФЧХ разомкнутой системы.

Размыкание системы принципиально может осуществляться в любом месте. Однако при исследовании устойчивости системы удобнее размыкать ее по цепи главной обратной связи.

Для применения критерия Найквиста система уравнений приводится к следующему виду.

- передаточная функция разомкнутой системы (прямой ветви).

Если разомкнутая система устойчива, то замкнутая система устойчива, если АФЧХ разомкнутой системы не охватывает критическую точку с координатами .

Для построения АФЧХ достаточно вызвать команду nyquist:

>> nyquist(w4)

На рис. 4.1.2.1 приведена АФЧХ разомкнутой системы (объекта регулирования).

Рис. 4.1.2.1 АФЧХ разомкнутой системы

Замкнутая система устойчива, так как АФЧХ разомкнутой системы не охватывает критическую точку с координатами .

Определение запасов устойчивости системы по модулю и по фазе

Для нормального функционирования любая система регулирования должна быть достаточно удалена от границы устойчивости. О запасе устойчивости можно судить по расположению корней характеристического полинома замкнутой системы. Чем дальше отстают корни этого полинома от мнимой оси, тем больше запас устойчивости.

Самое читаемое:

Информационно-вычислительная сеть на основе архитектуры клиент-сервер, предметная область Магазин бытовой техники
Компьютерная сеть обозначает наборы связанных между собой автономных компьютеров. Два компьютера называются связанными между собой, если они могут обмениваться информацией. Связь не обязательно должна осуществляться при помощи медного провода. Могут использоваться самые разнообразные средства связи, включая волоконную оптику, ...