Разделы сайта

Выбор средств и описание метода для исследования электромагнитной обстановки в помещении

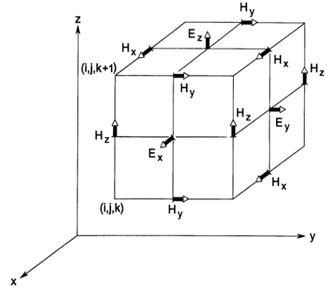
Рис. 2.3. Представление компонент поля в кубической ячейке

Примерно с 1990 г. метод конечных разностей стал основным для численного моделирования многих научных и инженерных задач, связанных с взаимодействием электромагнитных волн с объектами из разных материалов. Он может быть успешно применен для решения широкого спектра задач: от моделирования сверхдлинных электромагнитных волн в геофизики и микроволн (например, для расчёта характеристик антенн, разработки беспроводных устройств связи, в том числе цифровых) до решения задач в оптическом диапазоне.

Достоинства метода:

§ интуитивно понятен, поэтому пользователи могут легко понять, как он работает и каких результатов ждать от его применения в той или иной задаче.

§ работает во временной области, и соответственно, за один этап моделирования могут быть получены результаты в широком диапазоне частот, что исключает возможность потери резонансных пиков.

§ в методе поля вычисляются последовательно с течением времени, что позволяет создавать анимированные изображения распространения волновых процессов в расчетном объеме. Такие изображения могут быть очень полезны для понимания того, что происходит с моделью, и позволяют удостовериться, что модель работает корректно.

§ позволяет указать материал в каждой точке расчетного объема и может быть легко приспособлен для моделирования не только широкого спектра металлов и диэлектриков, но и материалов с нелинейными свойствами.

§ позволяет непосредственно моделировать эффекты на отверстиях, так же как эффекты экранирования, причем электромагнитные поля внутри и вне экрана могут быть рассчитаны напрямую или обратно.

§ сразу определяет значения векторов напряженности электрического E и магнитного H полей, знание которых необходимо для решения большинства задач ЭМС и электромагнитного взаимодействия, что очень удобно, так как оказывается ненужным промежуточное преобразование результатов моделирования.

Можно выделить следующие основные недостатки метода конечных разностей:

§ весь расчетный объем должен быть разбит на ячейки, и величина шага дискретизации должна быть достаточно малой по сравнению с наименьшей длиной волны, используемых в конкретной задаче объектов. Кроме того, эта величина определяет детализацию распределения материалов в пространстве. Поэтому может оказаться, что счетный объем должен быть разделен на очень большое число ячеек, что означает большие затраты памяти и большое время моделирования. Поэтому сложно моделировать задачи, с длинными, тонкими пространственными структурами, например, поля проводников с током.

§ метод конечных разностей рассчитывает электромагнитные поля в каждой точке расчётного объёма. Если требуется найти электромагнитное поле на некотором отдалении от источника, это, скорее всего, значит, что расчётный объем окажется чрезмерно большим. Существуют расширения метода для нахождения электромагнитных полей в дальней зоне, но они требуют постобработки.

§ расчётный объем должен быть конечным, чтобы уместиться в памяти компьютера. В большинстве случаев это достигается с помощью задания искусственных граничных условий. Но их нужно использовать с осторожностью, чтобы свести к минимуму вызываемые ими искажения. В настоящее время известно несколько эффективных граничных условий поглощения для алгоритма метода, позволяющих имитировать бесконечную расчетную область.

Метод конечных интегралов (FIT) представляет собой дискретную формулировку уравнений Максвелла в интегральной форме, удобную для реализации на компьютерах и позволяющую моделировать реальные электромагнитные задачи со сложной геометрией. Метод может быть реализован как во временной, так и в частотной области. Кроме того, не накладывается никаких ограничений на тип используемой сетки разбиения, наряду со структурированной сеткой в декартовой системе координат поддерживаются неортогональные сетки, например, тетраэдральная. Метод конечных интегралов имеет высокую эффективность в тех задачах, где необходим анализ нестационарных процессов в неоднородном, анизотропном пространстве для объектов с произвольной формой границ. Этот численный метод обеспечивает универсальную схему пространственной дискретизации, которую можно применять к различным случаям, начиная со статического поля и заканчивая высокочастотными расчетами во временной и частотной областях [24].

Перейти на страницу: 1 2 3 4

Самое читаемое:

Исследования свойств гексагональных кодирующих коллиматоров для однофотонной эмиссионной томографии
Цель работы: Численно исследовать аппаратные функции кодирующих коллиматоров, построенных на базе псевдослучайных последовательностей, расширенных псевдослучайных последовательностей, троичных последовательностей, расширенных троичных последовательностей. Оптимизировать скорость расчета аппаратных функций гексагональных кодирующих ...