Разделы сайта

Синтезировать структуру и параметры законов регулирования

Уравнение пропорционально интегрального дифференциального регулятора имеет вид:

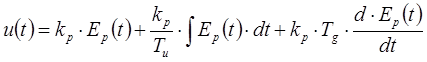
Типовые оптимальные процессы регулирования.

Характеристика переходного процесса, а следующее качество регулирования определяется в данных условиях выборным законом регулирования, так и настройки регулятора. При разных настройках можно получить различные переходные процессы, отличающиеся величиной перерегулирования и др. показатели качества. Оптимальными характеристикой процесса регулирования и необходимые настройки регулятора - понятия относительные. В зависимости от условий регулирования технологического процесса (и качества продукции), характеризуются возмущений и устройства аппаратуры регулирования, признаны различные процессы регулирования. В общем, случаи рекомендуется три процесса регулирования:

. Апериодический (граничный) процесс с min временем регулирования.

Характеризуется помимо min временем регулирования отсутствием перерегулирования и min регулирующим воздействием, т.е. min изменением подачи регулируемой среды. Последнее целесообразно в том случаи, когда регулируемое воздействие для рассматриваемой величины может оказывать влияние на другие величины.

. Процесс с 20% перерегулированием и min временем первого полупериода колебания.

Процесс с 20% перерегулированием рекомендуется в тех случаях, когда допустима известная величина, которая снижает max динамическое отклонение. Min время первого периода полу-колебания, в котором имеет место наибольшее место отклонение от заданного является преимуществом, если остальная часть процесса, где отклонение значений не велики менее существенна или несущественна вовсе.

. Процесс с min квадратной площадью отклонения (min y2dt).

Характеризуется наибольшим перерегулированием (40-45%) и временем регулирования, наибольшим регулирующим воздействием. Ему свойственно наименьшая величина max динамического отклонения (φ1)

В качестве типового оптимального процесса регулирования рассмотрим процесс с 20% перерегулированием, а в качестве регулятора - пропорционально интегральный регулятор, тогда согласно методики Копеловеча А.П. из книги «Автоматическое регулирование»

Перейти на страницу: 1 2

Самое читаемое:

Непрерывный и квантованный объекты управления в пространстве состояний
1. Задана линейная стационарная дискретная система (параметры непрерывных динамических звеньев в таблице 1 Приложения 2). и . Рисунок 1. Структурная схема линейной стационарной дискретной системы . Составить описание непрерывного объекта управления в пространстве состояний. . Выбрать период дискретности и ...